Algoritmo de cifrado Rivest, Shamir, Adleman (RSA)
usos
RSA, que lleva el nombre de estos inventores, es un algoritmo de cifrado que pertenece a la gran familia de la "criptografía asimétrica".
RSA se puede utilizar para garantizar:
- confidencialidad: solo el titular de la clave privada podrá leer el mensaje cifrado con la clave pública correspondiente.
- no alteración y no repudio: solo el propietario de la clave privada puede firmar un mensaje (con la clave privada). Por tanto, una firma descifrada con la clave pública demostrará la autenticidad del mensaje.
Su robustez radica en la dificultad de factorizar un gran número.
Eventos clave
- 1978: Ronald L. Rivest, Adi Shamir y Leonard Adleman publican "Un método para obtener firmas electrónicas y claves públicas de criptosistemas". En la revista mensual de la Association for Computing Machinery (ACM).
- 1982: Rivest, Shamir y Adleman fundaron la empresa "RSA Data Security" (que en 2006 se convirtió en "RSA, la división de seguridad de EMC"). "Un sistema criptográfico de comunicaciones y método". patentado en 1983 en el Instituto de Tecnología de Massachusetts (MIT), expiró en septiembre de 2000.
- 1991: publicación de los primeros “Estándares de Criptografía de Clave Pública” (PKCS), y apertura del “Concurso de factorización RSA” (cerrado en 2007), impulsando al mundo de la investigación a desarrollar métodos para factorizar claves públicas (y por tanto descifrar cualquier mensaje).
- 1994: “El algoritmo de tiempo polinomial para la factorización por computadora cuántica” de Peter Shor, teóricamente permite romper cualquier clave RSA. Sin embargo, ponerlo en práctica requiere una computadora cuántica (que ha reavivado un gran interés en este campo). En 2001, IBM logró la factorización cuántica de una clave RSA de 15 bits (experimento repetido en 2012).
- 2000: publicación de los estándares PKCS # 15, el más reciente hasta la fecha (en la versión 1.1).
- 2010: la clave RSA de 768 bits de la competencia de 1991 está descifrada; hasta la fecha, este es el mejor resultado (conocido públicamente) de factorizar una clave RSA. En nuestro país, la Referencia de Seguridad General recomienda el uso de claves de 2048 bits para el período 2010-2021.
Implementación de RSA
Descargo de responsabilidad: este artículo establece el principio básico del algoritmo publicado en 1978.
Para una implementación rigurosa, se deben tomar en cuenta una cierta cantidad de precauciones para evitar ciertas vulnerabilidades (consultar los estándares más recientes).
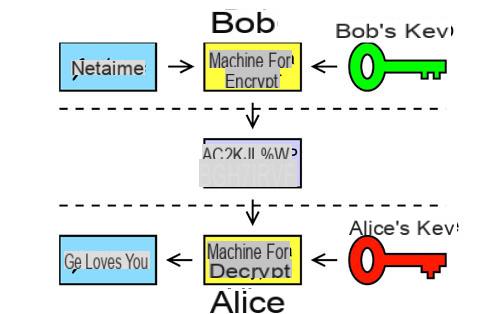
Alice y Bob
- Bob tiene un mensaje confidencial que quiere enviarle a Alice.
- Alice construye dos claves:
- una clave de cifrado pública que transmite a Bob.
- una clave de descifrado privada que guarda cuidadosamente.
- Bob usa la clave pública para cifrar el mensaje y se lo pasa a Alice.
- Alice usa la clave privada para descifrar el mensaje recibido.
Generación de claves
- Sean dos números primos grandes elegidos "al azar": py q.
- Nota: n = p * q y φ = (p-1) * (q-1)
- Dejemos que un todo grande sea elegido "al azar", primero con φ. Y la inversa de d módulo φ.
- La clave de cifrado pública es el par (n, e), la clave de descifrado privada es el par (n, d).
Cifrado / Descifrado
Cifrado
- Antes de ser encriptado, el mensaje original debe descomponerse en una serie de números enteros M con valores entre 0 y n-1.
- Para cada entero M tenemos que calcular C≡M ^ e [n].
- El mensaje cifrado se compone de la sucesión de números enteros C.
Descifrado
- De acuerdo con la forma en que fue encriptado, el mensaje recibido debe estar compuesto por una sucesión de números enteros C con valores entre 0 y n-1.
- Para cada entero C es necesario calcular M≡C ^ d [n].
- A continuación, el mensaje original se puede reconstruir a partir de la serie de números enteros M.
Fiabilidad
La seguridad del algoritmo RSA se basa en la dificultad de factorizar n.
Para descifrar el mensaje, es necesario encontrar d conociendo e, lo que requiere volver a calcular φ y, por lo tanto, conocer pyq, los dos factores primos de n.
Sin embargo, la factorización de un número entero (de tamaño muy grande) en factores primos es sumamente difícil, requiriendo esta operación una capacidad de cálculo muy importante.
Por ejemplo: en 2010, INRIA y sus socios lograron factorizar una clave de 768 bits. Les tomó dos años y medio de investigación y más de 10 ^ 20 cálculos. Este es el resultado de factorización más conocido hasta la fecha.
Para protegerse contra el aumento de la potencia informática, se recomienda regularmente utilizar tamaños de clave cada vez más grandes (actualmente 2048 bits).