Rivest, Shamir, Adleman (RSA) encryption algorithm
uses
RSA, named after these inventors, is an encryption algorithm belonging to the large “asymmetric cryptography” family.
RSA can be used to ensure:
- confidentiality: only the owner of the private key will be able to read the message encrypted with the corresponding public key.
- non-alteration and non-repudiation: only the owner of the private key can sign a message (with the private key). A signature decrypted with the public key will therefore prove the authenticity of the message.
Its robustness lies in the difficulty of factoring a large number.
Key events
- 1978: Ronald L. Rivest, Adi Shamir and Leonard Adleman publish "A Method for Obtaining Electronic Signatures and Public Keys from Cryptosystems." In the Association for Computing Machinery (ACM) monthly magazine.
- 1982: Rivest, Shamir and Adleman found the company "RSA Data Security" (which in 2006 became "RSA, The Security Division of EMC"). "A cryptographic system of communications and method." patented in 1983 at the Massachusetts Institute of Technology (MIT), it expired in September 2000.
- 1991: publication of the first “Public Key Cryptography Standards” (PKCS), and opening of the “RSA factorization competition” (closed in 2007), prompting the research world to develop methods for factorizing public keys (and therefore decrypt any message).
- 1994: “The polynomial time algorithm for quantum computer factorization” by Peter Shor, theoretically allows to break any RSA key. However, putting it into practice requires a quantum computer (which has rekindled a keen interest in this field). In 2001, IBM succeeded in quantum factorization of a 15-bit RSA key (experiment repeated in 2012).
- 2000: publication of the PKCS # 15 standards, the most recent to date (in version 1.1).
- 2010: the 768-bit RSA key from the 1991 competition is cracked, to date this is the best (publicly known) result of factoring an RSA key. In Our country, the General Security Reference recommends the use of 2048-bit keys for the period 2010-2021.
RSA implementation
Disclaimer: This article sets out the basic principle of the algorithm published in 1978.
For a rigorous implementation, a certain number of precautions must be taken into account in order to avoid certain vulnerabilities (refer to the most recent standards).
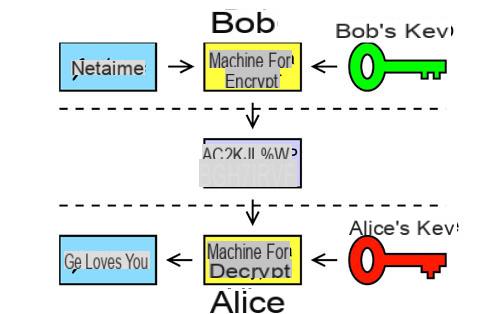
Alice and bob
- Bob has a confidential message he wants to send to Alice.
- Alice constructs two keys:
- a public encryption key which she transmits to Bob.
- a private decryption key that it keeps carefully.
- Bob uses the public key to encrypt the message, and passes it on to Alice.
- Alice uses the private key to decrypt the received message.
Key generation
- Let be two large prime numbers "randomly" chosen: p and q.
- Note: n = p * q and φ = (p-1) * (q-1)
- Let a large whole be "randomly" chosen, first with φ. And the inverse of d modulo φ.
- The public encryption key is the pair (n, e), the private decryption key the pair (n, d).
Encryption / Decryption
Encryption
- Before being encrypted, the original message must be decomposed into a series of integers M with values between 0 and n-1.
- For each integer M we have to calculate C≡M ^ e [n].
- The encrypted message is made up of the succession of integers C.
Decryption
- In accordance with the way in which it was encrypted, the received message must be composed of a succession of integers C with values between 0 and n-1.
- For each integer C it is necessary to calculate M≡C ^ d [n].
- The original message can then be reconstructed from the series of integers M.
Reliability
The security of the RSA algorithm relies on the difficulty of factoring n.
To decrypt the message, it is necessary to find d knowing e, which requires recomputing φ, and therefore knowing p and q, the two prime factors of n.
However, the factorization of an integer (of very large size) in prime factors is extremely difficult, this operation requiring a very important capacity of calculation.
For example: in 2010, INRIA and its partners succeeded in factoring a 768-bit key. It took them two and a half years of research, and over 10 ^ 20 calculations. This is the best known factorization result to date.
In order to guard against increasing computing power, it is regularly recommended to use increasingly large key sizes (currently 2048 bits).